
Funktionsname |
Funktion (Berechnung aus hypergeometrischer Funktion) |
Umkehrfunktion (inverse Function) |
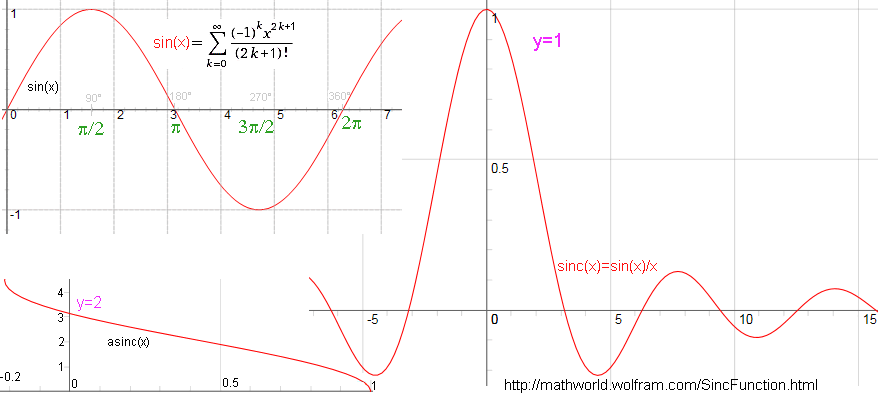
| Sinus | sin(x)=x*hyg0F1(3/2, -x²/4) Berechnungsbeispiel | asin(x)=atan(x/sqrt(1-x²))=x*hyg2F1(1/2,1/2,3/2,x²) |
| Kardinalsinus=Sinus cardinalis | sinc(x)=sin(x)/x=hyg0F1(3/2, -x²/4) | asinc(x)=inverse(r) Kardinalsinus |
| Kosinus | cos(x)=hyg0F1(1/2, -x²/4) online nachrechnen | acos(x)=PI/2-asin(x)=PI/2-x*hyg2F1(1/2,1/2,3/2,x²) |
| Sinus Hyperbolicus | sinh(x) = (exp(x)-exp(-x))/2=x*hyg0F1(3/2,x²/4) | asinh(x)= log(x+sqrt(x²+1))=x*hyg2F1(1/2,1/2,3/2,-x²) |
| Tangens | tan(x) = sin(x)/cos(x)=x*hyg0F1(3/2, -x²/4)/hyg0F1(1/2,-x²/4)=8x*hyg3F2[1,1/2-x/Pi,1/2+x/Pi,3/2-x/Pi,3/2+x/Pi,1]/(Pi²-4x²) | atan(x)=(x<1)? x*hyg2F1(1,1/2,3/2,-x²)else PI/2-hyg2F1(1/2,1,3/2,-1/x²)/x; Berechnungsbeispiel |
| Tangens Hyperbolicus | tanh(x) =(exp(2x)-1)/(exp(2x)+1)=8x*hyg3F2[1,1/2-x*i/Pi,1/2+x*i/Pi,3/2-x*i/Pi,3/2+x*i/Pi,1]/(Pi²+4x²) | atanh(x)= log((1+x)/(1-x))/2=x*hyg2F1[1,1/2,3/2,x²] |
| Kotangens | cot(x) = 1/tan(x) = 2*hyg3F2[1,-x/Pi,x/Pi,1-x/Pi,1+x/Pi,1]/x-1/x | acot(x)= PI/2-atan(x)=hyg2F1[1,1/2,3/2,-1/x²]/x |
| Exponentialfunktion | exp(x) Iterationsrechner Beispiel 11 | log(x)=(x-1)*hyg2F1(1,1,2,1-x) Iterationsrechner Beispiel 12 |
| Exponentialfunktion mal x | exp(x)*x = x*hyg1F1(1,1,x) | LambertW(x)=ProductLog(x) Iterationsrechner mit Unteriteration ; Beispiele |
| Potenz- & Wurzelfunktionen | pow(x,y)=x^y=exp(y*log(x))=hyg2F1(-y,1/1000,1/1000,1-x) | Potenz y fest: pow(x,1/y)= y. Wurzel von x siehe Beispiel 15 Basis x fest: log(x, Basis y)=log(x)/log(y) |
| Basis & Potenz gleich | pow(x,x)=x^x=exp(x*log(x))=hyg2F1(-x,1/1000,1/1000,1-x) | log(x)/LambertW(-½±½,log(x)) |
| Realteil einer komplexen Potenz :-) | Re((x+y*i)^z) = (x²+y²)^(z/2)*cos(z*atan(y/x)); z.B. Re(sqrt(2+3i))=1.674... x=2;y=3;z=0.5 | |
| Imaginärteil einer komplexen Potenz | Im((x+y*i)^z) = (x²+y²)^(z/2)*sin(z*atan(y/x)) | |
| Fakultät | x!=Fak(x)=Gamma(x+1) | aFak(x) siehe Regula falsi & Beispiel 35 |
| Doppelfakultät (Double Factorial) | x!!=DblFak(x)=2^(1/4+x/2-cos(PI*x)/4)*PI^(cos(PI*x)/4-1/4)*Gamma(x/2+1) | aDblFak(x):=y-(4(y!!-x))/(y!!(2Digamma(y/2+1)+pi*log(2/pi)*sin(pi*y)+log(4))) |
| Subfakultät (Subfactorial=Derangement) | !x=SubFak(x)=Gamma(x+1,-1)/e | aSubFak(x)... in Arbeit |
| Gammafunktion (Eulersches Integral 2. Gattung) | Gamma(x)=(x-1)! | aGamma(x)=aFak(x)+1 |
| Digammafunktion=Psi-Funktion | Digamma(x)=(x-1)*hyg3F2(1,1,2-x,2,2,1)-[A001620] siehe DigammaFunction | aDigamma(x) siehe Regula falsi & Beispiel 35 |
| Harmonische Zahl (HarmonicNumber) | HarmonZahl(x)=Digamma(x+1)+[A001620] siehe Harmonische Reihe | aHarmonZahl(x) ... in Arbeit... |
| Integralexponentialfunktion | Ei(x) siehe Integralexponentialfunktion | aEi(x):=y-(Ei(y)-x)*y/exp(y); nach Newton und Simpson |
| Gaußsche Fehlerfunktion | erf(x) siehe Beispiele 41 bis 43 | aerf(x) online per Iterationsrechner berechnen |
| imaginäre Fehlerfunktion | erfi(x) = 2*x*hyg1F1(1/2, 3/2, x²)/Sqrt(Pi) siehe auch wolfram Erfi | aerfi(x) in Arbeit... |
| Dawson`s Integral | Dawson(x) = erfi(x)*Sqrt(Pi)*exp(-x²)/2 siehe DawsonsIntegral | aDawson(x) in Arbeit... |
| Gudermannfunktion | Gudermann(x) siehe Iterationsrechner Beispiel 39 | aGudermann(x) siehe Iterationsrechner Beispiel 40 |
| vollständige elliptische Integral 1. Art | EllipticK(x)= PI*hyg2F1(1/2,1/2,1,x)/2 = PI/2/agm(1,sqrt(1-x)) | ...in Arbeit... |
| vollständige elliptische Integral 1. Art | EllipticF(x,y)=[h=x*hyg0F1(3/2,-x²/4)]*AppellF1(1/2,1/2,1/2,3/2,h²,y*[h]²) | ... |
| vollständige elliptische Integral 2. Art | EllipticE(x)=PI*hyg2F1(-1/2,1/2,1,x)/2 siehe Elliptische Integrale | ...in Arbeit... |
| vollständige elliptische Integral 2. Art | EllipticE2(x,y)=[h=x*hyg0F1(3/2,-x²/4)]*AppellF1(1/2,1/2,-1/2,3/2,h²,y*[h]²) | ... |
| Stieltjes-Konstanten | siehe Stieltjes-Konstanten und Stieltjes Constants | ...in Arbeit... |
| Riemannsche Zeta-Funktion | siehe Riemannsche Zeta-Funktion und RiemannZetaFunction | ...in Arbeit... |
| Fibonacci-Funktion | Fibonacci(x) siehe Iterationsrechner Beispiel 8 | aFibonacci(x) siehe Iterationsrechner Beispiel 96 |
| Fibonacci Polynome (Polynomial) | FibonacciPoly(x,y)=(((y+sqrt(4+y²))/2)^x-(2/(y+sqrt(4+y²)))^x *cos(x*PI))/sqrt(4+y²) siehe wolfram hyper2F1 | |
| Arithmetisch-geometrisches Mittel | agm(x,y)=(x+y)/2/hyg2F1(1/2,1/2,1,((y-x)/(x+y))²) siehe Iterationsrechner Beispiel 1 | |
| Kubische Analogie von AGM | agm3(x,y) siehe Iterationsrechner | |
| AGM mit Wichtung | agmW3(x,y,z) siehe Iterationsrechner a=x;b=y;d=Wichtung | |
| Quadratische Iteration | agm4(x,y) siehe Quadratic Iteration Iterationsrechner berechnen | |
| Caveat Emptor | agmCaveat(x,y) siehe Caveat Emptor Iterationsrechner berechnen | |
| Hölder-Mittel (generalized mean) | HoelderMW(x,y,z) siehe Mittelwerte z=-1=harm. z=0=geom. z=1=arithm. z=2=quadratischer Mittelwert; z>0 beliebig reell | |
| Bessel-Funktionen 1. Gattung | BesselJ(x,y)=(y/2)^x*hyg0F1(x+1,-y²/4)/Gamma(x+1) siehe BesselJ Diagramm und BesselFunctionoftheFirstKind | |
| Bessel-Funktionen 2. Gattung | BesselY(x,y) siehe BesselFunctionoftheSecondKind | |
| modifizierte Bessel-Funktionen 1. Gattung | BesselI(x,y) siehe ModifiedBesselFunctionoftheFirstKind | |
| modifizierte Bessel-Funktionen 2. Gattung | BesselK(x,y) siehe x<>Int(x) und x==Int(x) per 3 hypergeometrischer Funktionen!! | |
| Bruchannäherung | GetBruchNenner(x,y=NennerMax) genauer als Approximation von Dezimalbrüchen durch echte Brüche | |
| unvollständige Gammafunktion der oberen Grenze | Gamma1(x,y)=γ(x,y)=Gamma(x)-Gamma2(x,y) siehe lower incomplete gamma function | |
| unvollständige Gammafunktion der unteren Grenze | Gamma2(x,y)=Γ(x,y) siehe Incomplete Gamma Function | |
| Binomialkoeffizient | binom(x,y)=x!/y!/(x-y)! siehe Binomialkoeffizient z.B. binom(Pi,e)=1.903568... | |
| exklusives ODER ( Kontravalenz ) | x XOR y Beispiel: [A086202]=1/PI XOR 1/(2PI)=0.4756... PlouffesConstants | wenn x XOR y = Erg, dann -> x= y XOR Erg und y= x XOR Erg |
| Pochhammer Symbol | pochhammer(x,y)=Gamma(x+y)/Gamma(x) siehe PochhammerSymbol | |
| hypergeometrische Funktion mit 2 Parametern | hyg0F1(x,y) siehe Hypergeometrische Funktion und Hypergeometric0F1 | |
| hypergeometrische Funktion mit 3 Parametern | hyg1F1(x,y,z) siehe Hypergeometrische Funktion und Hypergeometric1F1 | |
| hypergeometrische Funktion mit 4 Parametern | hyg2F1(x,y,z,h) siehe Iterationsrechner Beispiel 70 und Hypergeometric2F1 | |
| Appell hypergeometrische Funktion F1 mit 6 Parametern | AppellF1(x,y,z,h,M,N)=F111_100 siehe Wolfram AppellF1 | |
| Appell hypergeometrische Funktion F2 mit 7 Parametern | AppellF2(x,y,z,h,M,N1;N2)=F111_011 siehe Wiki Appell series | |
| Appell hypergeometrische Funktion F3 mit 7 Parametern | AppellF3(x,y,z,h,M,N1;N2)=F022_100(x,z,y,h,M,N1;N2) siehe Wiki Appell series | |
| Appell hypergeometrische Funktion F4 mit 6 Parametern | AppellF4(x,y,z,h,M,N)=F200_011 siehe Wiki Appell series | |
| KAMPÉ DE FÉRIET doppelt hypergeometrische Funktion (generalized Double Hypergeometric Series) | F012_201(x,y,z,h,M,N1;N2;N3) siehe KAMPÉ DE FÉRIET | |
| KAMPÉ DE FÉRIET doppelt hypergeometrische Funktion (generalized Double Hypergeometric Series) | F020_100(x,y,z,h,M) siehe KAMPÉ DE FÉRIET | |
| KAMPÉ DE FÉRIET doppelt hypergeometrische Funktion (generalized Double Hypergeometric Series) | F021_101(x,y,z,h,M,N1;N2) siehe KAMPÉ DE FÉRIET | |
| ErdelyiG G-Funktion (Erdélyi G-function) | ErdelyiG(x)=hyg2F1(1,x,x+1,-1)*2/x=Digamma(x/2+1/2)-Digamma(x/2) siehe mathworld G-Funktion | |
| Barnessche G-Funktion (Barnes G-function) | BarnesG(x) siehe Barnessche G-Funktion | |
| Polylogarithmus (Jonquière´s Polylogarithm) | PolyLog(x,y)=Li(x,y)=Sum[y^k/k^x]; {1<=k<Inf} siehe Polylogarithmus ; Dirichletsche Eta(x)=η(x)= -Li(x,y= -1) | |
| Eulersche Betafunktion (Beta function; Integral 1. Gattung) | Beta(x,y)=Gamma(x)*Gamma(y)/Gamma(x+y) siehe Eulersche_Betafunktion | |
| PowPowMod(x,y,z,h)=x^y^z mod h | 3^2014^2014 mod 98 = 25 oder 2^74207281^1 mod 1000000000000... und extrem größer (big Integer calculator) | |